niedziela, 13 stycznia 2013

2.3.8 Odchylenie standardowe

Jest to wartość przybliżająca jak bardzo wartości odbiegają od średniej. Używanym terminem jest również wariancja, jest to odchylenie stand. do kwadratu. Brane pod uwagę będą różnice pomiędzy kolejnymi wartościami xi i średnią, podniesione do kwadratu, tzn. \left (x_1-\bar x \right ) ^2.
Wariancja jest średnią arytmetyczną tychże kwadratów różnic pomiędzy wartościami a średnią. Obliczyć ją można z odchylenia (podnosząc je do kwadratu), wobec czego ograniczymy się do wzoru dla tej drugiej wartości. Oznaczamy jako s^2.
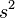Odchylenie standardowe
  • Dla danych zawierających tylko wartości lub wartości i ich liczności – używamy wzoru na średnią arytmetyczną kwadratów różnic, znajdującą się pod pierwiastkiem. W pierwszym przypadku, za 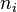n_i podstawiamy 1.
s = \sqrt{\frac{(x_1-\bar x)^2\ n_1 +...+ (x_k-\bar x)^2\ n_k}{n}}
n_i\,   -liczność danej klasy
\bar x   -średnia
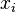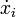
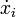  • W przypadku danych w postaci szerego rozdzielczego – używamy powyższego wzoru, w miejsce wartości x_i\, wstawiając środki klas \dot x_i
s = \sqrt{\frac{(\dot x_1-\bar x)^2\ n_1 +...+ (\dot x_k-\bar x)^2\ n_k}{n}}
\dot x_i   -środek i-tej klasy
Autor: o

Brak komentarzy:

Prześlij komentarz

Subskrybuj: Komentarze do posta (Atom)