niedziela, 13 stycznia 2013

1.7.2 Aproksymacja średniokwadratowa

Wprowadzenie do aproksymacji średniokwadratowej

W aproksymacji średniokwadratowej dla funkcji f(x) określonej w przedziale <a,b> poszukujemy minimum całki:
||F(x)-f(x)||=\int_a^bw(x)[F(x)-f(x)]^2dx\;
(2.4)
lub na zbiorze dyskretnym zamiast całki (2.4) poszukujemy minimum sumy:
||F(x)-f(x)||=\sum_{i=1}^nw(x_i)[F(x_i)-f(x_i)]^2\;

Omówienie aproksymacji średniokwadratowej

Poszukujemy funkcji aproksymującej, której to piszemy przy pomocy funkcji bazowej φi(x) i współczynników ai, przy czym te współczynniki są tak określone by (2.4) przyjmowało wartość minimalną, przy funkcji wagowej w(xj) większej od zera, wtedy napiśmy taką funkcję H przy naszych współczynnikach ai:
H(a_0,a_1,..,a_m)=\sum_{j=1}^nw(x_j)\left[f(x_j)-\sum_{i=0}^ma_i\varphi_i(x_j)\right]^2\;
(2.7)
Aby funkcja względem współczynników ai , czyli według (2.7) przyjmowała wartość ekstremalną, to wtedy musi zachodzić, że pochodna funkcji H (2.7) względem współczynników ak powinna być równa zero:
{{\partial H}\over{\partial a_k}}=0\mbox{, }k=0,1,2,..,m\;
(2.8)
Jesli do warunku na ekstremalną wartość funkcji H, czyli (2.8), względem współczynników ak wstawimy definicje funkcji H (2.7), otrzymujemy:
{{\partial H}\over{\partial a_k}}=-2\sum_{j=0}^nw(x_j)\left[f(x_j)-\sum_{i=0}^ma_i\varphi_i(x_j)\right]\varphi_k(x_j)=0\;
(2.9)
Równość (2.9) sugeruje, że można zdefiniować macierze:
\mathbf{D}=\begin{bmatrix} \varphi_0(x_0)&\cdots&\varphi_m(x_0)\\ \varphi_0(x_1)&\cdots&\varphi_m(x_1)\\ \cdots\\\cdots&\cdots&\cdots\\ \varphi_0(x_n)&\cdots&\varphi_m(x_n)\\ \end{bmatrix}\;
(2.10)
\mathbf{A}=\begin{bmatrix}a_0\\a_1\\\vdots\\a_m\end{bmatrix}\;
(2.11)
\mathbf{f}=\begin{bmatrix}f(x_0)\\f(x_1)\\\vdots\\f(x_n)\end{bmatrix}\;
(2.12)
Mając zdefiniowane macierze (2.10), (2.11) i (2.12) możemy napisać równość (2.9) w postaci macierzowej przy nieosobliwej macierzy D:
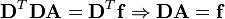
\mathbf{D}^T\mathbf{D}\mathbf{A}=\mathbf{D}^T\mathbf{f}\Rightarrow\mathbf{D}\mathbf{A}=\mathbf{f}\;
(2.13)
W wyniku aproksymacji średnio-kwadratowej otrzymujemy na podstawie (2.13), że iloczyn macierzy D (zdefiniowanej przy pomocy funkcji φi(xj)) przez wektor A (zdefiniowanej przy pomocy współczynników aproksymacji ai) jest równa wektorowi f (zdefiniowanej przy pomocy wartości funkcji f(xj) dla j=0,1,..,m).
Autor: o

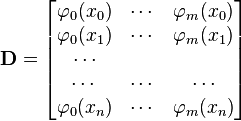
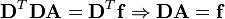
Brak komentarzy:

Prześlij komentarz

Subskrybuj: Komentarze do posta (Atom)