Metody numeryczne i probalistyczne: 1.2 Model obliczeniowy

Tworząc i analizując algorytmy, jakie będą pojawiać w naszym wykładzie, będziemy posługiwać się pewnym uproszczonym modelem obliczeń, dzięki czemu będziemy mogli skoncentrować się na esencji algorytmu, bez detali implementacyjnych --- zostawiając je na inną okazję (dobra implementacja konkretnego algorytmu może być sama w sobie interesującym wyzwaniem programistycznym; często bywa, że dobre implementacje, nawet prostych algorytmów numerycznych, są mało czytelne).
Aby zdefiniować nasz model obliczeniowy, posłużymy się pojęciem programu. Zastosujemy przy tym notację podobną do tej z języka programowania C.
Program składa się z deklaracji, czyli opisu obiektów, których będziemy używać, oraz z poleceń (instrukcji), czyli opisu akcji, które będziemy wykonywać.
Dostępnymi obiektami są stałe i zmienne typu całkowitego (int), rzeczywistego (float i double). Typ logiczny symulujemy tak jak w C wartościami zero-jedynkowymi typu całkowitego. Zmienne jednego typu mogą być grupowane w wektory albo tablice. Widzimy więc, że podstawowe algorytmy numeryczne będą bazować na mało skomplikowanych typach danych. Również nieskomplikowane będą instrukcje naszego modelowego języka. Dążenie do prostoty (ale nie za wszelką cenę) jest charakterystyczne dla numeryki. Typowe jest zastępowanie skomplikowanych tablic rekordów prostszymi macierzami, eleganckich rekurencji --- zwykłymi pętlami działającymi na danych w miejscu. Jedną z myśli przewodnich numeryki jest bowiem szybkość, a rezygnacja z barokowych konstrukcji językowych jest zgodna z filozofią architektury procesora RISC: efektywność przez prostotę.
(Na pewno zastanawiasz się teraz, jaka jest druga myśl przewodnia numeryki. To dokładność.)

Podstawienie

Najprostsza z instrukcji, bez której nie można się obejść:

z = <math>\displaystyle {\cal W}</math>;

Tutaj $\displaystyle z$ jest zmienną, a $\displaystyle {\cal W}$ jest wyrażeniem o wartościach tego samego typu co $\displaystyle z$ . Jest to polecenie proste.
Wyrażeniem jest pojedyncza stała lub zmienna, albo złożenie skończonej liczby operacji elementarnych na wyrażeniach. Operacje elementarne to:

arytmetyczno--arytmetyczne: $\displaystyle x\mapsto -x$ , $\displaystyle (x,y)\mapsto x+y$ ,

$\displaystyle (x,y)\mapsto x-y$ , $\displaystyle (x,y)\mapsto x*y$ , $\displaystyle (x,y)\mapsto x/y, y\ne 0$ , gdzie $\displaystyle x,y$ są stałymi lub zmiennymi liczbowymi,

arytmetyczno--logiczne: $\displaystyle (x,y)\mapsto x<y$ ,

$\displaystyle (x,y)\mapsto x\le y$ , $\displaystyle (x,y)\mapsto x=y$ , $\displaystyle (x,y)\mapsto x\ne y$ , gdzie $\displaystyle x,y$ są stałymi lub zmiennymi liczbowymi,

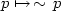logiczno--logiczne: $\displaystyle p\mapsto\,\sim \,p$ ,

$\displaystyle (p,q)\mapsto p\, \wedge \,q$ , $\displaystyle (p,q)\mapsto p\, \vee \,q$ , gdzie $\displaystyle p,q$ są stałymi lub zmiennymi logicznymi.
Dla niektórych zadań wygodnie jest uzupełnić ten zbiór o dodatkowe operacje, takie jak obliczanie wartości niektórych standardowych funkcji matematycznych ( $\displaystyle \sqrt{\;}, \cos(), \sin(), \exp(), \log(),$ itp.), czy nawet funkcji bardziej skomplikowanych. Na przykład, zastosowanie "szkolnych" wzorów na obliczanie pierwiatków równania kwadratowego byłoby niemożliwe, gdyby pierwiastkowanie było niemożliwe.

Uwaga

Należy pamiętać, że w praktyce funkcje standardowe (o ile są dopuszczalne) są obliczane przy użyciu czterech podstawowych operacji arytmetycznych. Dokładniej, jednostka arytmetyczna procesora potrafi wykonywać jedynie operacje $\displaystyle +,\,-,\,\times,\,\div$ , przy czym dzielenie zajmuje kilka razy więcej czasu niż pozostałe operacje arytmetyczne. Niektóre procesory (np. Itanium 2) są w stanie wykonywać niejako jednocześnie operację dodawania i mnożenia (tzw. FMADD, fused multiply and add). Praktycznie wszystkie współczesne procesory mają także wbudowany koprocesor matematyczny, realizujący asemblerowe polecenia wyznaczenia wartości standardowych funkcji matematycznych ( $\displaystyle \sqrt{\;}, \cos(), \sin(),\exp(), \log(),$ itp.), jednak wykonanie takiej instrukcji wymaga mniej więcej kilkadziesiąt razy więcej czasu niż wykonanie operacji dodawania.

Uwaga

Niestety, aby nasz model obliczeniowy wiernie odpowiadał rzeczywistości, musimy w nim uwzględnić fakt, że nawet podstawowe działania arytmentyczne (i, tym bardziej, obliczanie wartości funkcji matematycznych) nie są wykonywane dokładnie. Czasem uwzględnienie tego faktu wiąże się ze znaczącym wzrostem komplikacji analizy algorytmu i dlatego "w pierwszym przybliżeniu" często pomija się to ograniczenie przyjmując model, w którym wszystkie (lub prawie wszystkie) działania arytmetyczne wykonują się dokładnie. Wiedza o tym, kiedy i jak zrobić to tak, by wciąż wyciągać prawidłowe wnioski odnośnie faktycznej realizacji algorytmów w obecności błędów zaokrągleń jest częścią sztuki i wymaga intuicji numerycznej, popartej doświadczeniem.

Mamy trzy podstawowe polecenia złożone: warunkowe, powtarzania i kombinowane.

Warunkowe

if(<math>\displaystyle \cal W</math>) 
 <math>\displaystyle {\cal A}_1</math>;
else
 <math>\displaystyle {\cal A}_2</math>;

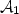gdzie $\displaystyle {\cal W}$ jest wyrażeniem o wartościach całkowitych (0 odpowiada logicznemu fałszowi, inne wartości --- logicznej prawdzie), a $\displaystyle {\cal A}_1$ i $\displaystyle {\cal A}_2$ są poleceniami, przy czym dopuszczamy polecenia puste.

Powtarzane

while(<math>\displaystyle {\cal W}</math>)
 <math>\displaystyle {\cal A}</math>;

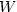gdzie $\displaystyle W$ jest wyrażeniem o wartościach logicznych, a 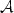$\displaystyle \cal A$ jest poleceniem.

Kombinowane

{
 <math>\displaystyle {\cal A}_1;\displaystyle {\cal A}_2;\displaystyle \ldots\displaystyle {\cal A}_n;</math>
}

gdzie $\displaystyle {\cal A}_j$ są poleceniami.
Na podstawie tych trzech poleceń można tworzyć inne, takie jak pętle for(), czy instrukcje wariantowe switch(), itd.
Mamy też dwa szczególne polecenia, które odpowiadają za "wejście" i "wyjście".

Wprowadzanie danych

<math>\displaystyle {\cal IN}</math>(x,t);

gdzie $\displaystyle x$ jest zmienną rzeczywistą, a $\displaystyle t$ "adresem" pewnego funkcjonału $\displaystyle L:F\toR$ należącym to pewnego zbioru $\displaystyle T$ . W wyniku wykonania tego polecenia w zmiennej $\displaystyle x$ zostaje umieszczona wartość $\displaystyle L_t(f)$ .
Polecenie to pozwala zdobyć informację o danej $\displaystyle f$ . Jeśli $\displaystyle F=R^n$ to zwykle mamy $\displaystyle T=\{1,2,\ldots,n\}$ i $\displaystyle L_i(f)=f_i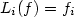$ , co w praktyce odpowiada wczytaniu $\displaystyle i$ -tej współrzędnej wektora danych. W szczególności, ciąg poleceń $\displaystyle {\cal IN}(x[i],i)$ , $\displaystyle i=1,2,\ldots,n$ , pozwala uzyskać pełną informację o $\displaystyle f$ . Jeśli zaś $\displaystyle F$ jest pewną klasą funkcji $\displaystyle f:[a,b]\toR$ , to możemy mieć np. $\displaystyle T=[a,b]$ i $\displaystyle L_t(f)=f(t)$ . W tym przypadku, wykonanie polecenia $\displaystyle {\cal IN}(x,t)$ odpowiada w praktyce skorzystaniu ze specjalnej procedury (albo urządzenia zewnętrznego) obliczającej (mierzącego) wartość funkcji $\displaystyle f$ w punkcie $\displaystyle t$ .

Wyprowadzanie wyników

<math>\displaystyle {\cal OUT}</math>(<math>\displaystyle {\cal W}</math>);

gdzie $\displaystyle {\cal W}$ jest wyrażeniem o wartościach rzeczywistych. Polecenie to pozwala "wskazać" kolejną współrzędną wyniku.
Zakładamy, że na początku procesu obliczeniowego wartości wszystkich zmiennych są nieokreślone, oraz że dla dowolnych danych wykonanie programu wymaga wykonania skończonej liczby operacji elementarnych. Wynikiem obliczeń jest skończony ciąg liczb rzeczywistych (albo $\displaystyle puste$ ), którego kolejne współrzędne pokazywane są poleceniem $\displaystyle {\cal OUT}$

Metody numeryczne i probalistyczne

Strony

niedziela, 13 stycznia 2013

1.2 Model obliczeniowy